英文：binary search tree。

一、图例

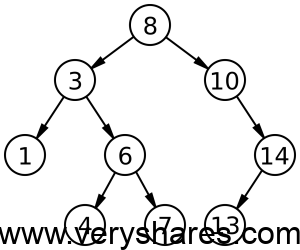
前序遍历：8 3 1 6 4 7 10 14 13

中序遍历：1 3 4 6 7 8 10 13 14

后序遍历：1 4 7 6 3 13 14 10 8

层次遍历：8 3 10 1 6 14 4 7 13

二、二叉树的构造

// 节点对象的构造函数
function Node (data, left, right) {
  this.data = data
  this.left = left
  this.right = right
}

Node.prototype.getData = function () {
  return this.data
}

// 二叉树的构造函数
function BST () {
  this.root = null
}

// 插入方法
BST.prototype.insert = function (data) {
  var n = new Node(data, null, null)
  if (this.root === null) {
    this.root = n
  } else {
    var current = this.root
    var parent
    while (true) {
      parent = current
      if (data < current.data) {
        current = current.left
        if (current === null) {
          parent.left = n
          break
        }
      } else {
        current = current.right
        if (current === null) {
          parent.right = n
          break
        }
      }
    }
  }
}

var nums = new BST()
nums.insert(8)
nums.insert(3)
nums.insert(10)
nums.insert(1)
nums.insert(6)
nums.insert(14)
nums.insert(4)
nums.insert(7)
nums.insert(13)

三、前/中/后序遍历（递归）

这个算法很好实现，主要是容易记混怎么样算前序遍历、中序遍历、后续遍历，其遍历顺序分别为：

• 前序遍历：根节点 > 左子树 > 右子树。
• 中序遍历：左子树 > 根节点 > 右子树。
• 后序遍历：左子树 > 右子树 > 根节点。

// 前序遍历二叉树
BST.prototype.preOrder = function (node) {
  if (node !== null) {
    console.log(node.getData())
    this.preOrder(node.left)
    this.preOrder(node.right)
  }
}

// 中序遍历二叉树
BST.prototype.inOrder = function (node) {
  if (node !== null) {
    this.inOrder(node.left)
    console.log(node.getData())
    this.inOrder(node.right)
  }
}

// 后序遍历二叉树
BST.prototype.postOrder = function (node) {
  if (node !== null) {
    this.postOrder(node.left)
    this.postOrder(node.right)
    console.log(node.getData())
  }
}

// 测试

nums.inOrder(nums.root)

// 依次输出如下内容：
// 1 3 4 6 7 8 10 13 14

四、前/中/后序遍历（非递归）

4.1、前序遍历的非递归实现

根据前序遍历访问的顺序，优先访问根结点，然后再分别访问左孩子和右孩子。 即对于任一结点，其可看做是根结点，因此可以直接访问，访问完之后，若其左孩子不为空， 按相同规则访问它的左子树；当访问其左子树时，再访问它的右子树。因此其处理过程如下：

对于任一结点P：

1. 访问结点P，并将结点P入栈;
2. 判断结点P的左孩子是否为空，若为空，则取栈顶结点并进行出栈操作，并将栈顶结点的右孩子置为当前的结点P，循环至1;若不为空，则将P的左孩子置为当前的结点P;
3. 直到P为NULL并且栈为空，则遍历结束。

function preOrder (bst) {
    let p = bst.root
    const arr = []
    while (p !== null || arr.length > 0) {
        while (p !== null) {
            console.log(p.getData())
            arr.push(p)
            p = p.left
        }

        if (arr.length > 0) {
            p = arr.pop()
            p = p.right
        }
    }
}

4.2、中序遍历的非递归实现

根据中序遍历的顺序，对于任一结点，优先访问其左孩子，而左孩子结点又可以看做一根结点， 然后继续访问其左孩子结点，直到遇到左孩子结点为空的结点才进行访问，然后按相同的规则访问其右子树。因此其处理过程如下：

对于任一结点P，

1. 若其左孩子不为空，则将P入栈并将P的左孩子置为当前的P，然后对当前结点P再进行相同的处理；
2. 若其左孩子为空，则取栈顶元素并进行出栈操作，访问该栈顶结点，然后将当前的P置为栈顶结点的右孩子；
3. 直到P为NULL并且栈为空则遍历结束。

function inOrder (bst) {
    let p = bst.root
    const arr = []
    while (p !== null || arr.length > 0) {
        while (p !== null) {
            arr.push(p)
            p = p.left
        }

        if (arr.length > 0) {
            p = arr.pop()
            console.log(p.getData())
            p = p.right
        }
    }
}

4.3、后序遍历的非递归实现

后续遍历比前中/序遍历是要麻烦一些的。

遍历顺序：左右根。左路的遍历和上面的思路是类似的，区别是元素出栈时不能直接打印， 因为如果有没访问过的右侧子树的话，需要先访问右侧子树。 右侧子树访问结束后才访问根（一些列子树的根）。

function postOrder (bst) {
    let p = bst.root
    let last = null
    const arr = []
    while (p !== null || arr.length > 0) {
        while (p !== null) {
            arr.push(p)
            p = p.left
        }

        if (arr.length > 0) {
            p = arr[arr.length - 1] // 栈顶元素
            // 当p不存在右子树或右子树已被访问过的话，直接访问当前节点数据
            if (!p.right || p.right === last) {
                p = arr.pop()
                console.log(p.getData())
                last = p // 记录上一次访问过的节点
                p = null // 这个容易漏掉，避免下个循环继续访问左子树
            } else {
                p = p.right
            }
        }
    }
}

五、参考资料

• 二叉树的非递归遍历